为了便于自己查找以前的一些绘图代码,对绘图代码进行了整理,放到自己的博客上来。
通用的头文件引入与设置
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False #减号
plt.rcParams['font.sans-serif'] = ['SimHei'] #中文字体
plt.rcParams['savefig.dpi'] = 300 #图片像素
plt.rcParams['figure.dpi'] = 300 #分辨率
盒图绘制
最常用的是seaborn结合dataframe的绘图方式。
dataFrame的样式如下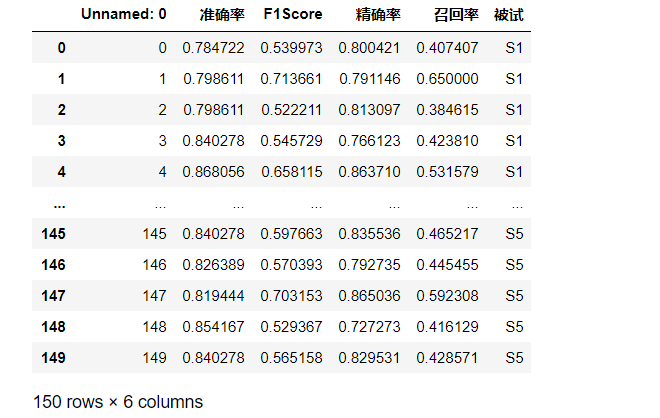
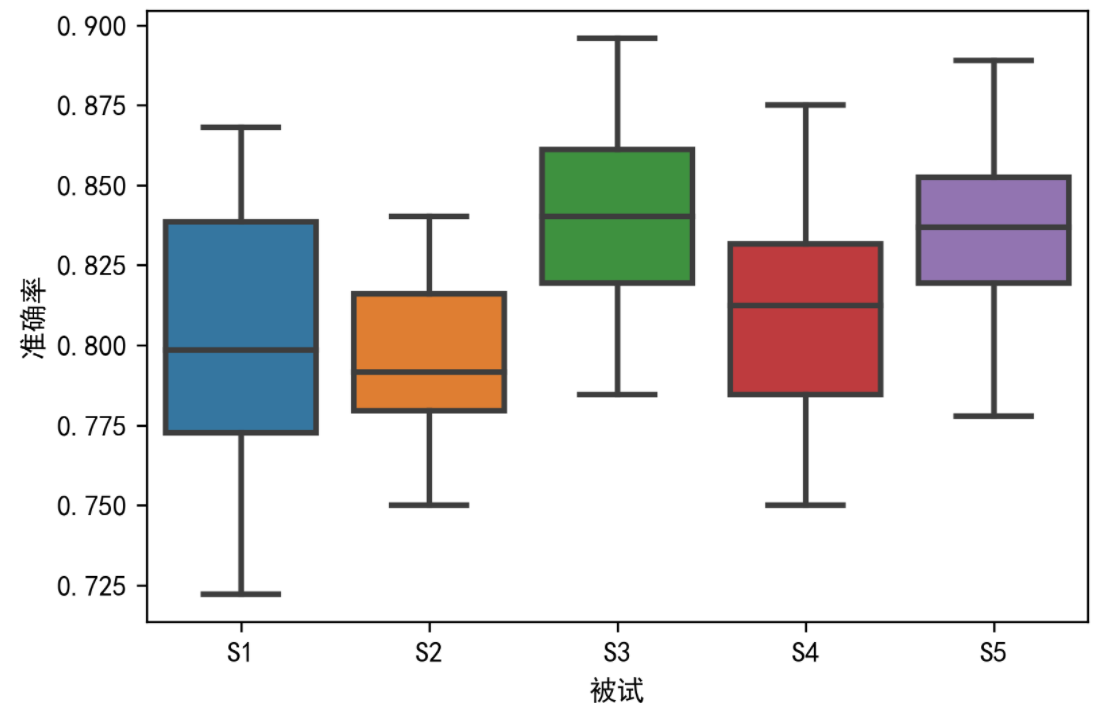
可以通过x来设置类别,y来设置所要展示的值的分布。
sns.boxplot(x="被试",y="准确率",data=df, linewidth=2)
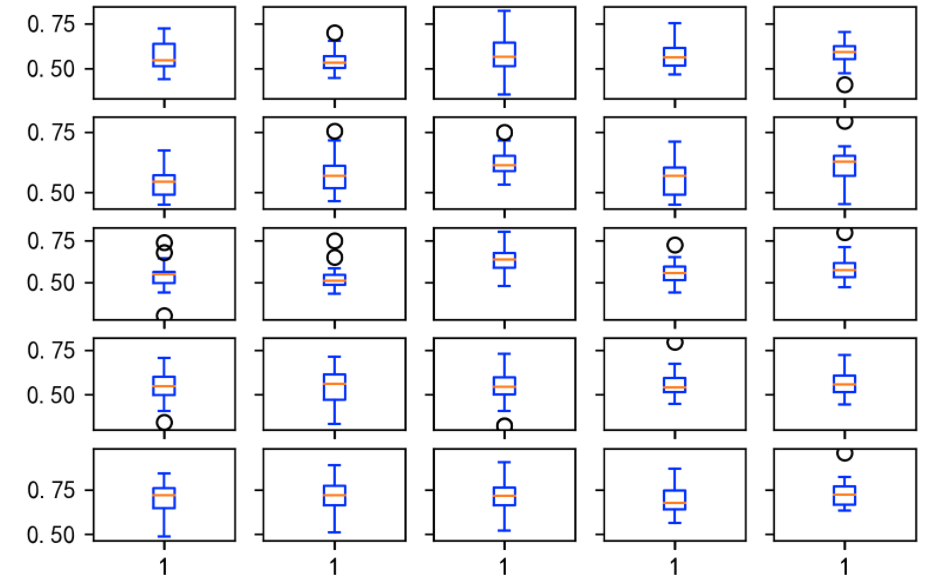
当然我们也可以尝试一个能从更高维度看数据分布的盒图。在这里面,通过sharex与sharey来实现了共享纵轴和横轴。
其中models[i]表示模型i,peoples[j]表示第j个被试。通过这两个维度来确定某个数值的分布。从而轻易的看到,什么模型在哪个人身上的表现良好。
fig,ax=plt.subplots(5,5,sharex="col",sharey="row")
for i in range(5):
for j in range(5):
people=peoples[j]
axt=ax[i,j]
data=models[i][models[i]["被试"]==people]
axt.boxplot(data["F1Score"].values,boxprops=dict(color="blue"),capprops=dict(color="blue"),whiskerprops=dict(color="blue"))
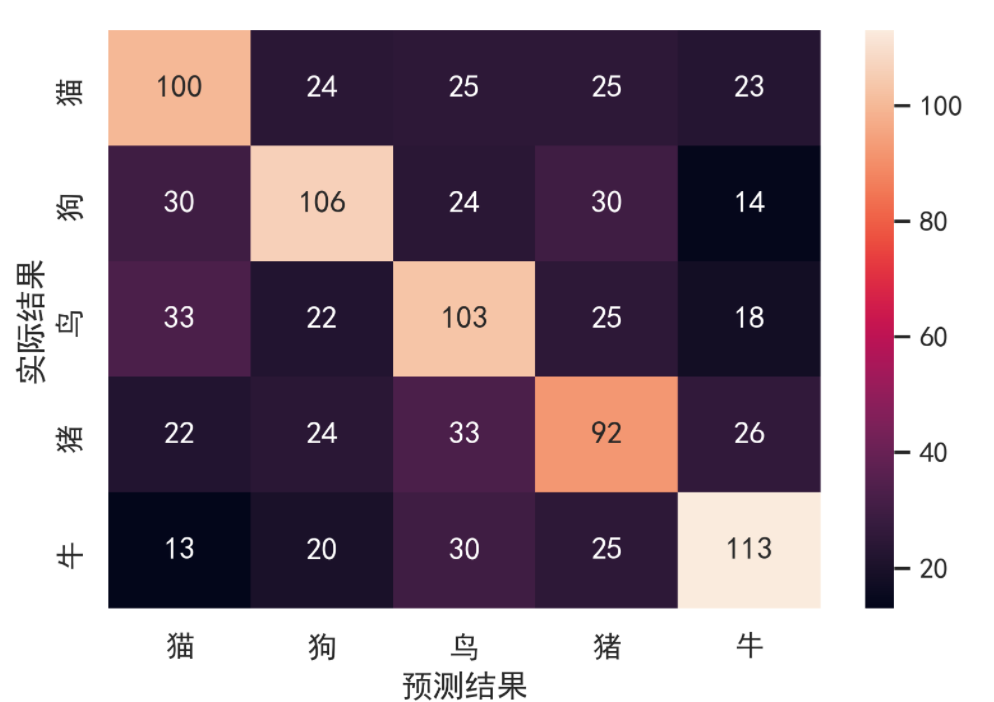
混淆矩阵的绘制(实质是热力图)
一般做多分类任务的时候会用到混淆矩阵,帮我们看看哪些类容易错分到哪些类。
#演示数据的生成
test_label=np.random.randint(0,5,(1000))
y_pred=np.random.randint(0,5,(1000))
#部分标签相同 表示预测正确
y_pred[:400]=test_label[:400]
names=["猫","狗","鸟","猪","牛"]
#计算混淆矩阵
C2= confusion_matrix(test_label,y_pred,[0,1,2,3,4])
#化成dataframe并且行列命名
df=pd.DataFrame(C2,index=names,columns=names)
#fmt='g'是指关闭科学计数法
sns.heatmap(df,annot=True,fmt='g')
plt.xlabel("预测结果")
plt.ylabel("实际结果")
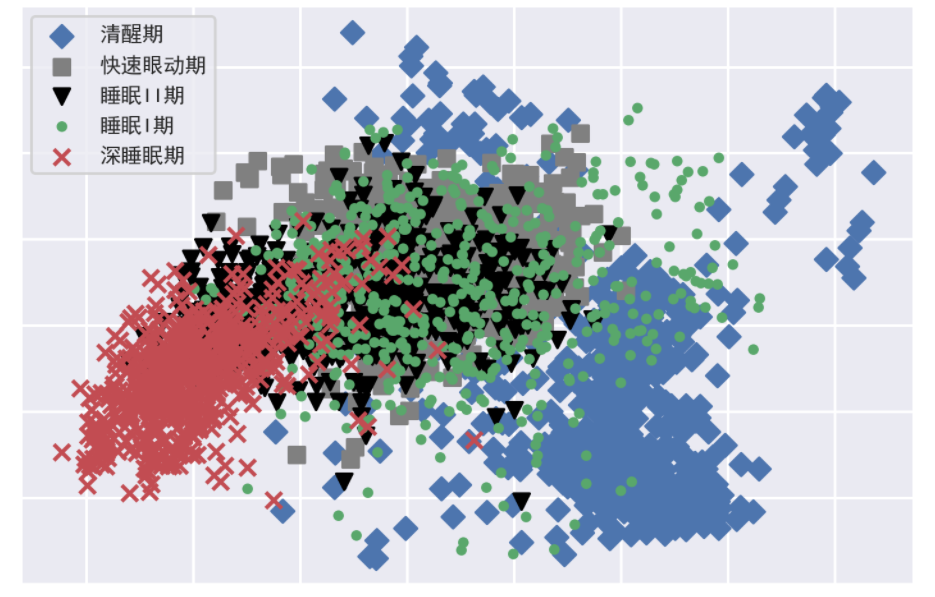
多分类中的散点图
这里面的x和y分别表示需要画的图的x坐标和y坐标,legend自动产生了图例并放到最好的位置。
plt.scatter(yellow_x, yellow_y, c='b', marker='D', label='清醒期')
plt.scatter(black_x, black_y, c='gray', marker='s', label='快速眼动期')
plt.scatter(blue_x, blue_y, c='black', marker='v', label='睡眠II期')
plt.scatter(green_x, green_y, c='g', marker='.', label='睡眠I期')
plt.scatter(red_x, red_y, c='r', marker='x', label='深睡眠期')
plt.legend(loc='best',prop = {'size':8})
plt.show()
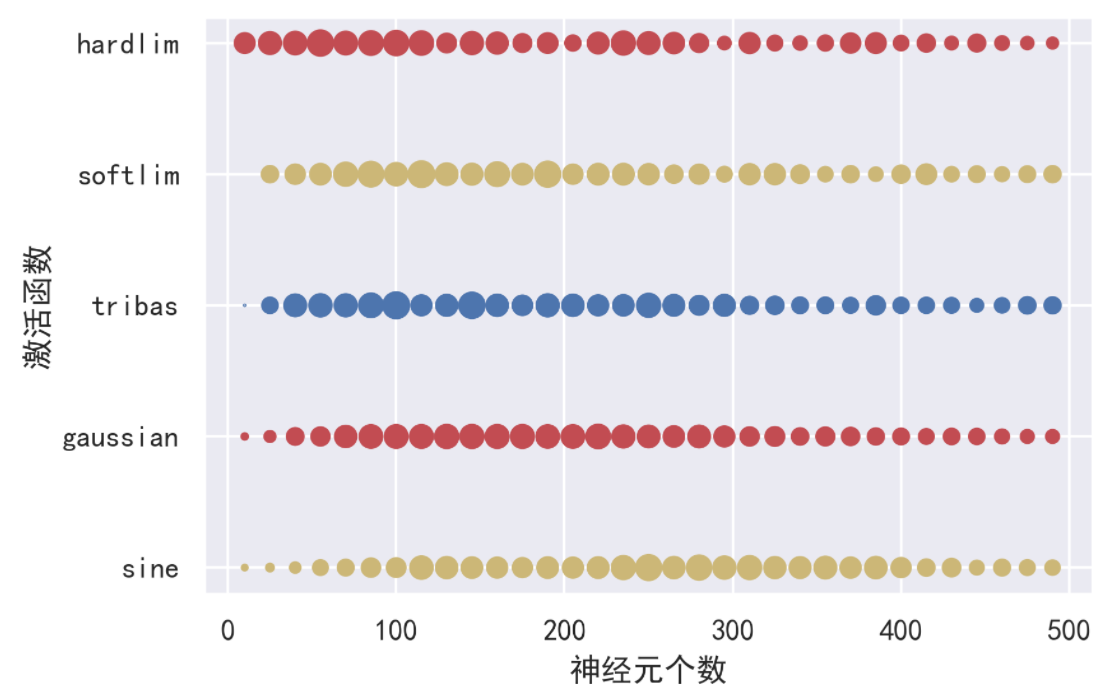
通过点的大小来表示因变量在不同条件下的动态变化
#trans表示一个转换函数,将所需要的值映射到一个合理的范围,使得点的大小能区分出因变量大小的变化。
plt.scatter(x,[0 for i in range(len(x))],s= trans(sine)*20,c='y')
plt.scatter(x,[1 for i in range(len(x))],s=trans(gaussian)*20,c='r')
plt.scatter(x,[2 for i in range(len(x))],s=trans(tribas)*20 )
plt.scatter(x,[3 for i in range(len(x))],s= trans(softlim)*20,c='y')
plt.scatter(x,[4 for i in range(len(x))],s=trans(hardlim)*20,c='r')
plt.yticks([0,1,2,3,4],labels=["sine","gaussian","tribas","softlim","hardlim"])
plt.ylabel("激活函数")
plt.xlabel("神经元个数")