欧式空间对齐的迁移学习[论文复现]

前段时间发现华科的迁移学习有点东西，就找了他们的论文来复现一下。
《Transfer Learning for Brain-Computer Interfaces: A Euclidean Space Data Alignment Approach》
DOI:10.1109/TBME.2019.2913914

这篇论文主要实现了一个简称EA(Euclidean Align)的迁移方法，和RA(Riemann Align),做了理论上的对比。同时做了迁移和不迁移的对比。实践证明确实有提示。

其原理主要是通过将每个被试的平均协方差矩阵变成单位矩阵，也就是将每个被试从自身所在域变化到了单位域。具体公式可以去看论文，这边主要是代码实现。

这一域变化的代码实现如下。

from functools import reduce
import numpy as np
#欧式空间对齐
def euclidAlign(X):
    #计算R矩阵
    R=np.zeros((X.shape[1],X.shape[1]))
#     for i in range(X.shape[0]):
#         R=R+np.dot(X[i,:,:],X[i,:,:].T)
    R=reduce(lambda R,y:R+np.dot(y,y.T),X,R)
    R=R/X.shape[0]
    for i in range(X.shape[0]):
        X[i,:,:]=np.dot(fuduiban(R),X[i,:,:])
    return X
#计算矩阵的负二分之一
def fuduiban(R):
    v, Q = np.linalg.eig(R)
    ss = np.diag(v ** (-0.5))
    #若出现异常值 就补充0
    ss[np.isnan(ss)] = 0
    re = np.dot(Q, np.dot(ss, np.linalg.inv(Q)))
    #取实数部分
    return np.real(re)

然后根据这个来下载了论文里说的RSVP数据集。
顺便写了一个便于操作的数据加载代码。

import mne
import numpy as np
from functools import lru_cache
from mne.io import concatenate_raws, read_raw_edf
mne.set_log_level(verbose="WARNING")

#单文件缓存加载
@lru_cache(maxsize=32)
def getDataByFileName(filename="5-Hz/rsvp_5Hz_03b.edf",log=False,ea=False):
    raw=read_raw_edf(filename,preload=False)
    raw.resample(64)
    events_from_annot, event_dict = mne.events_from_annotations(raw)
    nt=event_dict['T=0,x=-1']
    event_dict={'0': nt,'1': nt+1,}
    for item in events_from_annot:
        if item[2]>nt:
            item[2]=nt+1
    epochs = mne.Epochs(raw, events_from_annot, event_dict, 0, 0.7,baseline=None)
    d1=epochs['0'].copy().get_data()
    d2=epochs['1'].copy().get_data()
    if log:
        print(d1.shape,d2.shape)
    data=np.vstack([d1,d2])
    labels=np.array([0 if i<d1.shape[0] else 1 for i in range(d1.shape[0]+d2.shape[0]) ])
    #ea 表示是否使用EA做迁移
    if ea:
        data=euclidAlign(data)
    return data,labels
#多个路径的数据整合一起加载
def getDataByPaths(paths,log=False,ea=False):
    data=[]
    labels=[]
    for path in paths:
        tdata,tlabels=getDataByFileName(filename=path,log=log,ea=ea)
        data.append(tdata)
        labels.append(tlabels)
    data=np.vstack(data)
    labels=np.hstack(labels)
    return data,labels

然后是路径生成代码，主要是检查是否有这个文件。

import os
paths=[]
for i in range(1,15):
    path="5-Hz/rsvp_5Hz_%02da.edf"%(i)
    if os.path.exists(path):
        paths.append(path)
        path="5-Hz/rsvp_5Hz_%02db.edf"%(i)
        paths.append(path)
len(paths)

随便选一个基于xdawn的分类器。

from pyriemann.estimation import Xdawn
from mne.decoding import Vectorizer
from pyriemann.estimation import Shrinkage
from sklearn.pipeline import make_pipeline 

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
clf3 = make_pipeline(Xdawn(nfilter=3),
                    Vectorizer(),
                     LDA(solver="lsqr",shrinkage="auto",priors=[0.5,0.5]))

最后采用留一被试法来检验跨被试的效果，也就是每次都用10个被试训练，剩下一个被试测试
。

from sklearn.metrics import balanced_accuracy_score
#均衡准确率
res=[]
for i in range(11):
    trainP=[paths[j] for j in range(22) if j//2!=i ]
    testP=[paths[j]  for j in range(22) if j//2==i]
    print(testP)
    train_x,train_y=getDataByPaths(trainP,ea=True)#迁移与否在这里修改
    test_x,test_y = getDataByPaths(testP,ea=True)
    clf3.fit(train_x,train_y)
    y_pred=clf3.predict(test_x)
    res.append(balanced_accuracy_score(test_y, y_pred))
    print(res[-1])
print(np.mean(res))

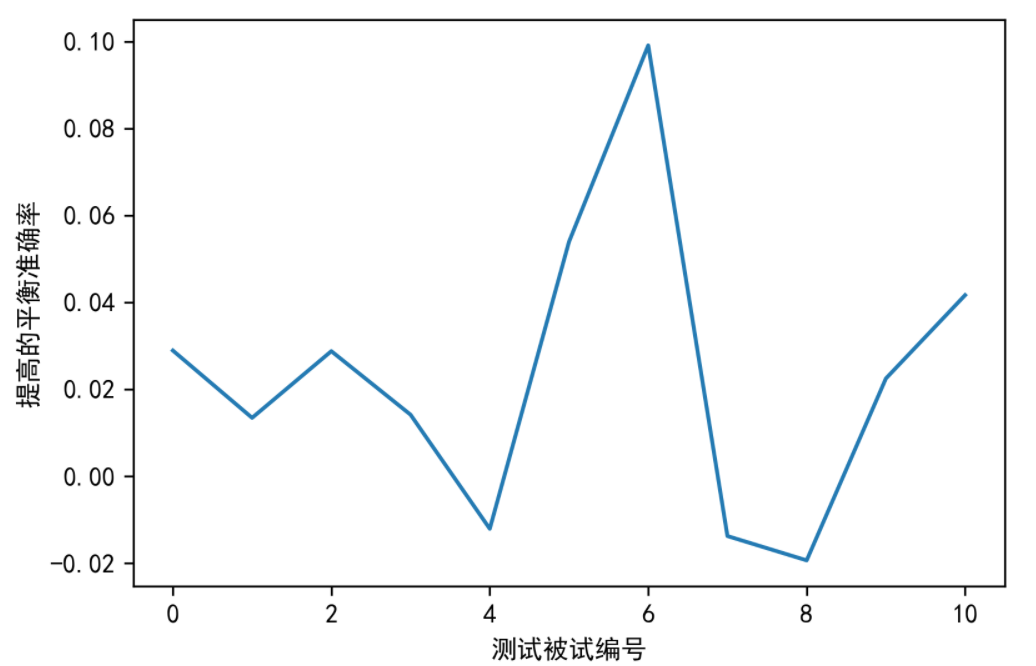
可以看到在多数被试上是有提升效果的。总的提升效果平均在2.2个百分点，虽然看起来不是特别多，但这个在实际中算是不小的提升了。

当然这个复现过程，使用的分类方法不太一样(主要是因为原文中所用方法的部分参数不知道，比如说xDAWN的滤波器数量、PCA降维的维数、SVM的参数等)，最终结果还比原文的稍微好点。