脑机接口(BCI)使用神经活动作为控制信号,实现与计算机的直接通信。这种神经信号通常是从各种研究透彻的脑电图(EEG)信号中挑选出来的。卷积神经网络(CNN)主要用来自动特征提取和分类,其在计算机视觉和语音识别领域中的使用已经很广泛。CNN已成功应用于基于EEG的BCI;但是,CNN主要应用于单个BCI范式,在其他范式中的使用比较少,论文作者提出是否可以设计一个CNN架构来准确分类来自不同BCI范式的EEG信号,同时尽可能地紧凑(定义为模型中的参数数量)。
前言
我们在后面的讲述中以单个脑电图为例,追寻单个脑电图在EEGNet中的变化。C表示channel即通道数,T表示times,准确的说是对应样本的采样点数量。
第一部分 时间卷积

这一部分主要用了F1个(1,64)的卷积核,对时间层面进行了卷积,其填充方式为’same’故最终时间维度的长度没有变。其张量变换如下。
- 输入张量(1,C,T)
- 卷积核形状(1,64)
- 卷积核数量F1
- 卷积核参数F1*64
- 输出张量(F1,C,T)
- BatchNorm
这一层对时间上的信息进行了融合,提取了F1种时间维度上的信息。
第二部分 空间卷积
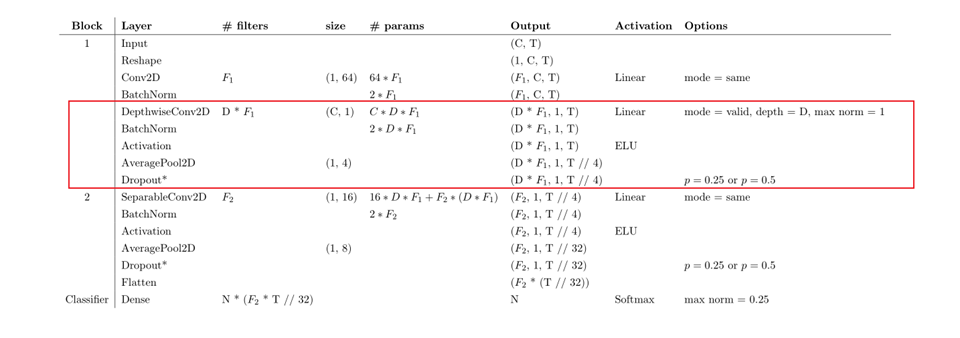
这一部分有一个非常有意思的东西,叫做深度卷积(Depthwise Convolution),在接触EEGNet之前我对深度卷积也是只闻其声不见其人。深入了解了它后面的产物深度可分离卷积,再次感叹前人的智慧无穷,还得多看论文。它卷积核的形状是(C,1)负责对各个空间(不同位置电极的输入)的信息进行整合,填充方式选择了”valid”。其张量变换如下。
- 输入张量(F1,C,T)
- 卷积核形状(C,1)
- 卷积核数量 D*F1
- 卷积核的参数 CDF1
- 输出张量(D*F1,1,T)
- BatchNorm
这边有个相较于普通卷积不同的地方,普通卷积从F1个核变化到DF1个核需要 F1D F1个卷积核。而深度卷积只用了DF1个卷积核。其区别在哪里呢?得到的信息又会有什么不同呢?下面就来带大家看看二者的区别。
普通卷积
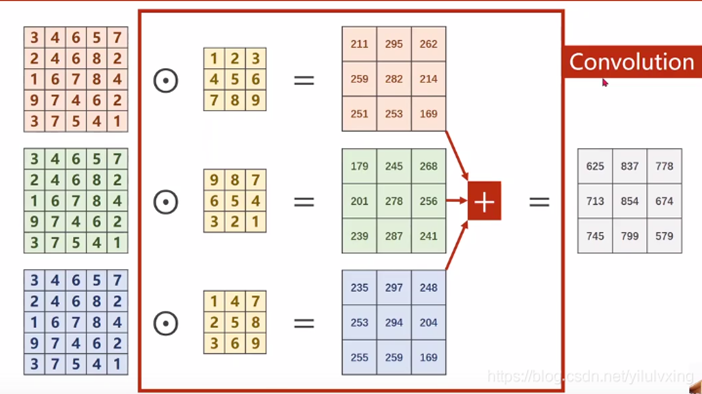
从图中可以看到,普通卷积的每个通道都要经过一个不一样的卷积核卷积,然后对得到的所有得到的数据进行相加得到一个新的通道。也就是说普通卷积得到新一层的每个通道都整合了上一层网络中所有通道的信息。
对于每个输出的通道都需要一组与原通道数量相同的卷积核来进行卷积。
深度卷积
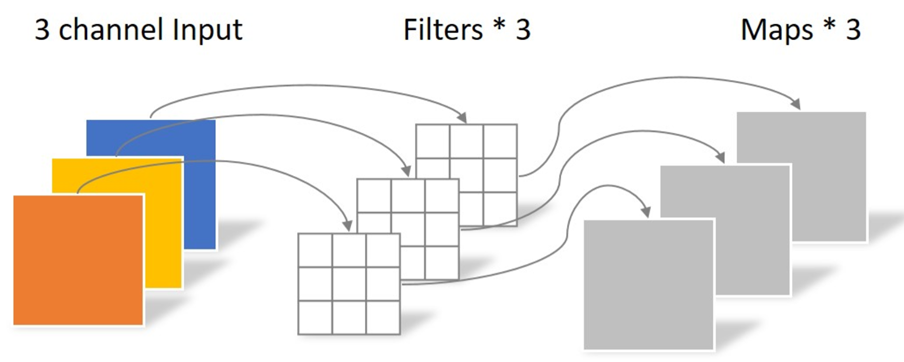
从图中可以看出,深度卷积的每个通道在经过卷积核之后,没有相加的操作,也就是说一个输出的通道对应一个输入的通道,当然也可以多个输出的通道对应一个输入的通道,在EEGNet里面就有体现,深度卷积里面D就是说D个输出的通道对应一个输入的通道。换句话说,我们对同一个通道进行了D次信息提取。
在EEGNet的实例中对比

激活函数与平均池化
经过激活函数ELU并且平均池化。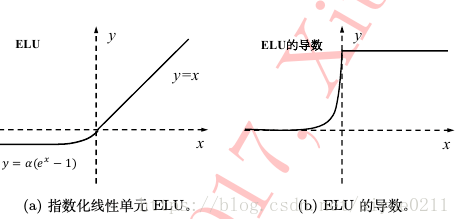
张量变换如下
- 输入张量(D*F1,1,T)
- 池化形状(1,4)
- 池化步长(1,4)
- Dropout p=0.25,p=0.5
- 输出张量(D*F1,1,T//4)
第三部分 深度可分离卷积
EEGNet论文中结构如下。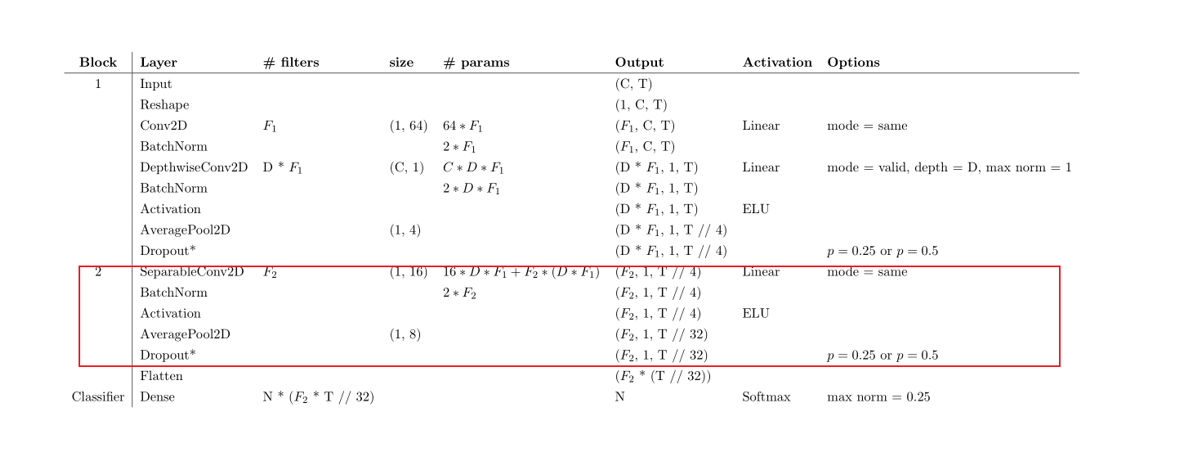
假设我们现在的目标是从三个通道转换到四个通道。
普通卷积
普通卷积的操作是下面这样的。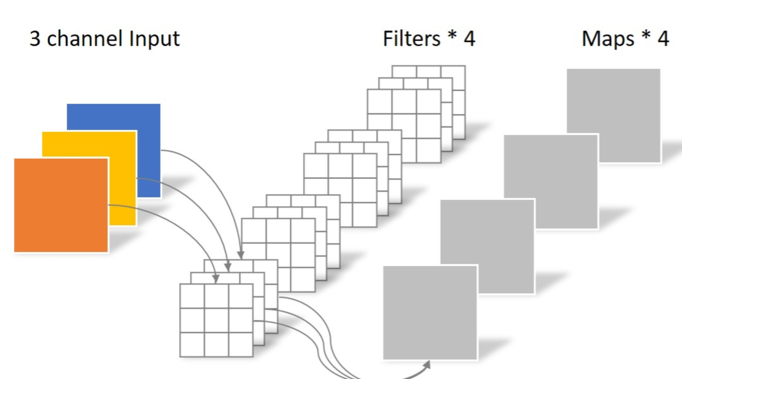
前面有提到,每个输出通道对应一组卷积核,总共需要43个共12个33卷积核。
深度可分离卷积
这个卷积分成两步。第一步就是前面提到的深度卷积,第二步就是带有1*1卷积核的普通卷积。
如果仅仅只走第一步,那么存在两个问题。首先,输出通道的数量不对,我们的目标是要4个通道,但是它只有3个通道;其次,输出通道只包含了对应输入通道的信息,没有包含所有输入通道的信息,没有起到信息整合的作用。所以第二步就显得尤为重要。
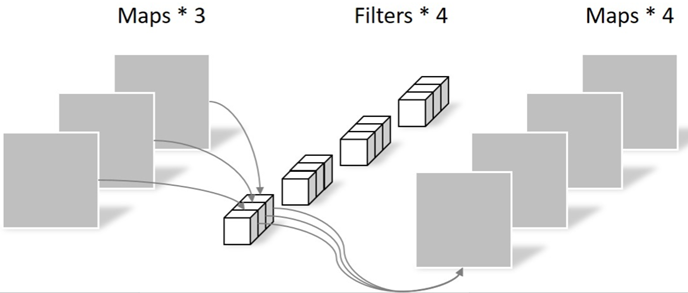
引入了1*1卷积核的普通卷积,对通道的数量进行转换的同时整合了输入通道的信息。
在EEGNet的实例中对比
同样是需要将输入的张量从(D*F1,1,T//4) 转换到(F2,1,T//4)。
普通卷积所需参数计算如下。
- (1,16)形状卷积核
- F2组卷积核每组D*F1个
- 输出张量(F2,1,T//4)
- 所需参数F2D F1*16
深度可分离卷积所需的参数计算如下:
- 第一步卷积:
- (1,16)形状卷积核
- D*F1组 每组1个
- 输出张量(D*F1,1,T//4)
- 所需参数DF116
- 第二步卷积:
- 使用(1,1)形状卷积核进行卷积
- F2组卷积核 每组D*F1个
- 输出张量(F2,1,T//4)
- 所需参数F2D F111
- 共需参数DF1 16+F2D F1
把一个乘法变成了加法,从而减少了所需的参数数量。
剩余部分
剩下的部分简单说一下,大家也都会。
将前面得到的张量归一化,并使用ELU激活函数激活
池化部分
- 输入张量(F2,1,T//4)
- 池化形状(1,8)
- 池化步长(1,8)
- Dropout p=0.25 or p=0.5
- 输出张量(F2,1,T//32)
全连接层(不含Bias)
- 输入张量(F2,1,T//32)
- Reshape To(F2*(T//32))
- 输出张量N(class_num)
- 所需参数数量NF2(T//32)
- 激活函数Softmax
复现EEGNet
import paddle.fluid as fluid
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph import Pool2D, Linear, Dropout, BatchNorm
from paddle.nn import Conv2D
class EEGNet(fluid.dygraph.Layer):
"""
EEGNet 暂未加入weight正则化 max norm 1 and 0.25
"""
def __init__(self, name_scope,ch_nums=16,T=250,class_dim=2):
"""
构造函数
"""
super(EEGNet, self).__init__(name_scope)
self.F1 = 16
self.D = 2
self.kern = 25
self.p = 0.25
self.F2 = 16*2 #self.F1*self.D #可自定义
self.fcin = self.F2*(T//32)
#第一层 时间卷积
self.conv1 = Conv2D(1, self.F1, (1,self.kern), padding="SAME")
self.bn1 = BatchNorm(self.F1)
#第二层 空间卷积
self.conv2 = Conv2D(self.F1,self.D*self.F1,(ch_nums,1),padding="VALID",groups=self.F1) #max norm 1
self.bn2 = BatchNorm(self.F1*self.D)
self.pool2 = Pool2D(pool_size=(1,4),pool_stride=(1,4),pool_type='avg')
# clip = fluid.clip.GradientClipByNorm(clip_norm=1.0)
#第三层 可分离卷积
self.conv3_1 = Conv2D(self.F1*self.D,self.F1*self.D,(1,16),padding="SAME",groups=self.F1*self.D)
self.conv3_2 = Conv2D(self.F1*self.D,self.F2,(1,1))
self.bn3 = BatchNorm(self.F2)
self.pool3 = Pool2D(pool_size=(1,8),pool_stride=(1,8),pool_type='avg')
self.fc = fluid.dygraph.Linear(input_dim=self.fcin, output_dim=class_dim, act='softmax') #max norm 0.25
def forward(self, x):
"""前向计算"""
# 第一层
x=self.conv1(x)
x=self.bn1(x)
# x=fluid.layers.dropout(x,0.25)
# x=fluid.layers.transpose(x,[0,3,1,2])
#第二层
x=self.conv2(x)
x=self.bn2(x)
x=fluid.layers.elu(x)
x=self.pool2(x)
x=fluid.layers.dropout(x,self.p)
#第三层
x=self.conv3_2(self.conv3_1(x))
x=self.bn3(x)
x=fluid.layers.elu(x)
x=self.pool3(x)
x=fluid.layers.dropout(x,self.p)
# 全连接层
out = fluid.layers.reshape(x, [-1, self.fcin])
out = self.fc(out)
return out
对于tensorflow实现的版本,EEGNet论文作者早已给出,也不需要我来给了。这边我用paddlepaddle复现了一下EEGNet,并且在百度的AIStudio上也有公开的项目供大家参考,如果有什么错误的地方也欢迎指出。
项目地址