用支持向量机处理快速序列视觉呈现的脑电信号

脑电信号 RSVP 事件相关电位
发布日期:   2020-09-10
文章字数:   2.1k
阅读次数:  

RSVP(Rapid Serial Visual Presentation,快速序列视觉呈现)是一种基于视觉图像序列刺激的实验范式,本文在处理脑机合作进行目标检测过程中的脑电信号,判断每段脑电信号中是否存在事件相关电位P300。

基本信息

  • 一共进行了12段。
  • 每段160张图片，每张图片1s，每段休息20s，即每一段3分钟。
  • 默认采样率1000

基本目标

大脑协助机器进行目标检测，从脑电信号中获取的信息有尽可能高的精确率(预测为正的样本中有多少是真正的正样本)，在精确率高的情况下，提高召回率(样本中的正例有多少被预测正确了)。

初始化

这边无需多说,主要包括引入头文件，设置生成图片的像素，真实目标序列，鼠标点击时间。

import mne
from mne.datasets import sample
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

plt.rcParams['savefig.dpi'] = 300 #图片像素
plt.rcParams['figure.dpi'] = 300 #分辨率
target_list = [
    [45, 80, 87, 117, 122, 128, 133, 138, 142, 150],
    [19, 28, 52, 59, 64, 85, 92, 99, 126, 133, 140, 145, 150],
    [10, 15, 21, 28, 40, 45, 51, 64, 70, 77, 83, 99, 111, 122, 139],
    [6, 17, 21, 59, 86, 112, 119, 123, 128, 138, 144],
    [34, 38, 52, 58, 71, 85, 91, 100, 106, 125],
    [9, 16, 22, 27, 32, 54, 69, 97, 140, 147, 154, 159],
    [5, 23, 28, 75, 80, 86, 90, 106, 113, 125],
    [21, 38, 45, 74, 91, 104, 110, 116, 137, 142, 148],
    [5, 23, 27, 32, 72, 77, 83, 102, 111, 116, 121, 126, 147, 154],
    [7, 75, 80, 90, 96, 101, 105, 128, 135, 141, 145, 152],
    [28, 37, 43, 50, 57, 65, 76, 87, 92, 103, 124],
    [12, 18, 25, 51, 57, 62, 75, 79, 91, 108, 114, 119, 125, 143, 149],
    [5, 13, 22, 28, 54, 90, 95, 120, 128, 138, 142, 147, 152, 156],
    [24, 31, 55, 96, 103, 116, 121, 126, 136, 143],
    [5, 67, 80, 85, 91, 102, 112, 118, 125, 131, 142],
    [4, 20, 51, 55, 60, 65, 71, 75, 82, 90, 95, 100, 104, 122, 130],
    [22, 28, 34, 41, 48, 53, 69, 73, 80, 104, 136],
    [9, 19, 35, 64, 71, 76, 81, 87, 93, 98, 105, 110, 135, 152],
    [18, 23, 30, 34, 72, 77, 82, 109, 117, 122, 130, 135, 141, 151],
    [43, 48, 70, 91, 98, 117, 122, 131, 138, 143, 147, 153],
    [30, 37, 42, 47, 56, 62, 68, 121, 132, 137, 144, 148, 153],
    [13, 26, 45, 50, 75, 90, 94, 98, 111, 117, 130, 144, 149],
]
clicktime=[45742,80509,87469,117526,122621,128597,133558,138445,142533,150414,199438,208661,214542,232581,239781,244533,265605,272565,279597,306557,313581,320517,325413,330621,370477,375453,381494,388477,400629,405509,411620,424484,430620,437716,443476,459461,471485,482661,499453,546493,557542,561517,599605,652573,659509,663517,668461,678614,684526,754597,758517,772494,778581,791797,805653,811740,814557,820661,826469,845797,909581,916517,922493,927589,932516,954628,969676,1040509,1047692,1054452,1059773,1085468,1103556,1108636,1155660,1160524,1166691,1170483,1186476,1193804,1205564,1281468,1298564,1305812,1334724,1335172,1341332,1351516,1364612,1370468,1376676,1397573,1402756,1408548,1445685,1463596,1467476,1472532,1512524,1517764,1523420,1542492,1551436,1556436,1561484,1566492,1587532,1594532,1627556,1695595,1700515,1710619,1716547,1721564,1725451,1748468,1755491,1761621,1765451,1772467,1828644,1837507,1843419,1850587,1857443,1865499,1876483,1887572,1892595,1903604,1924627,999999999999999]
filename = './data/P300_XH_Real.cnt'

数据加载函数

可以自定义数据路径，加载后降采样到什么程度，用什么程度的滤波，使用哪些电极通道等等。

def load_data(filename,sig_rate,drop_channels,low_f,up_f):
    raw = mne.io.read_raw_cnt(filename,preload=True)
    raw.drop_channels(drop_channels)
    raw.filter(low_f,up_f,fir_design='firwin')
    raw.resample(sig_rate)
    raw.plot_psd()
    return raw[:,:]

数据加载

这里总共有三种配置，用三种配置分别加载数据，看看哪个结果好。
这里我使用配置二（其他的都试过了，配置二相对好）。

配置一

  • 21导联 [P7,P5,P3,P1,PZ,P2,P4,P6,P8,PO7,PO5,PO3,POZ,PO4,PO6,PO8,CB1,O1,OZ,O2,CB2]
  • 降采样至200HZ，2-70Hz滤波
tot_channel=['FP1', 'FPZ', 'FP2', 'AF3', 'AF4', 'F7', 'F5', 'F3', 'F1', 'FZ', 'F2', 'F4', 'F6', 'F8', 'FT7', 'FC5', 'FC3', 'FC1', 'FCZ', 'FC2', 'FC4', 'FC6', 'FT8', 'T7', 'C5', 'C3', 'C1', 'CZ', 'C2', 'C4', 'C6', 'T8', 'M1', 'TP7', 'CP5', 'CP3', 'CP1', 'CPZ', 'CP2', 'CP4', 'CP6', 'TP8', 'M2', 'P7', 'P5', 'P3', 'P1', 'PZ', 'P2', 'P4', 'P6', 'P8', 'PO7', 'PO5', 'PO3', 'POZ', 'PO4', 'PO6', 'PO8', 'CB1', 'O1', 'OZ', 'O2', 'CB2', 'HEO', 'VEO', 'EKG', 'EMG']
need_channel=['P7','P5','P3','P1','PZ','P2','P4','P6','P8','PO7','PO5','PO3','POZ','PO4','PO6','PO8','CB1','O1','OZ','O2','CB2']
drop_channels=[ item for item in tot_channel  if item not in need_channel]
sig_rate=200
data,times=load_data(filename,sig_rate,drop_channels,2,70)

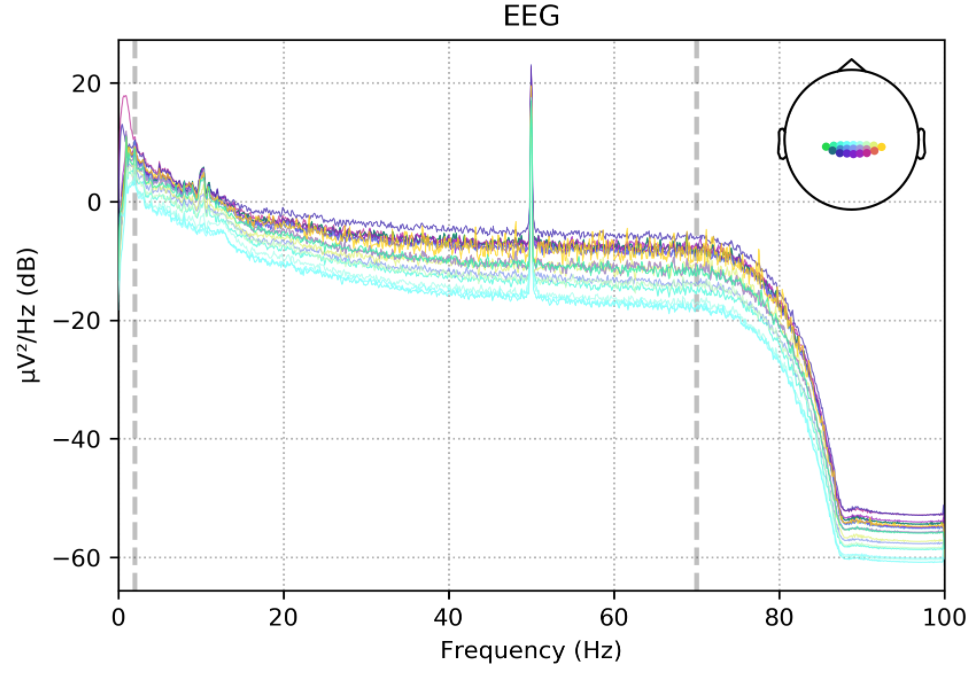
配置一功率谱密度图

配置二

  • 16导联 [FZ,FC1,FC2,C3,CZ,C4,CP1,CP2,P7,P3,PZ,P4,P8,O1,OZ,O2]
  • 降采样至32Hz,1-12Hz滤波
tot_channel=['FP1', 'FPZ', 'FP2', 'AF3', 'AF4', 'F7', 'F5', 'F3', 'F1', 'FZ', 'F2', 'F4', 'F6', 'F8', 'FT7', 'FC5', 'FC3', 'FC1', 'FCZ', 'FC2', 'FC4', 'FC6', 'FT8', 'T7', 'C5', 'C3', 'C1', 'CZ', 'C2', 'C4', 'C6', 'T8', 'M1', 'TP7', 'CP5', 'CP3', 'CP1', 'CPZ', 'CP2', 'CP4', 'CP6', 'TP8', 'M2', 'P7', 'P5', 'P3', 'P1', 'PZ', 'P2', 'P4', 'P6', 'P8', 'PO7', 'PO5', 'PO3', 'POZ', 'PO4', 'PO6', 'PO8', 'CB1', 'O1', 'OZ', 'O2', 'CB2', 'HEO', 'VEO', 'EKG', 'EMG']
need_channel=['FZ','FC1','FC2','C3','CZ','C4','CP1','CP2','P7','P3','PZ','P4','P8','O1','OZ','O2']
drop_channels=[ item for item in tot_channel  if item not in need_channel]
sig_rate=32
data,times=load_data(filename,sig_rate,drop_channels,1,12)

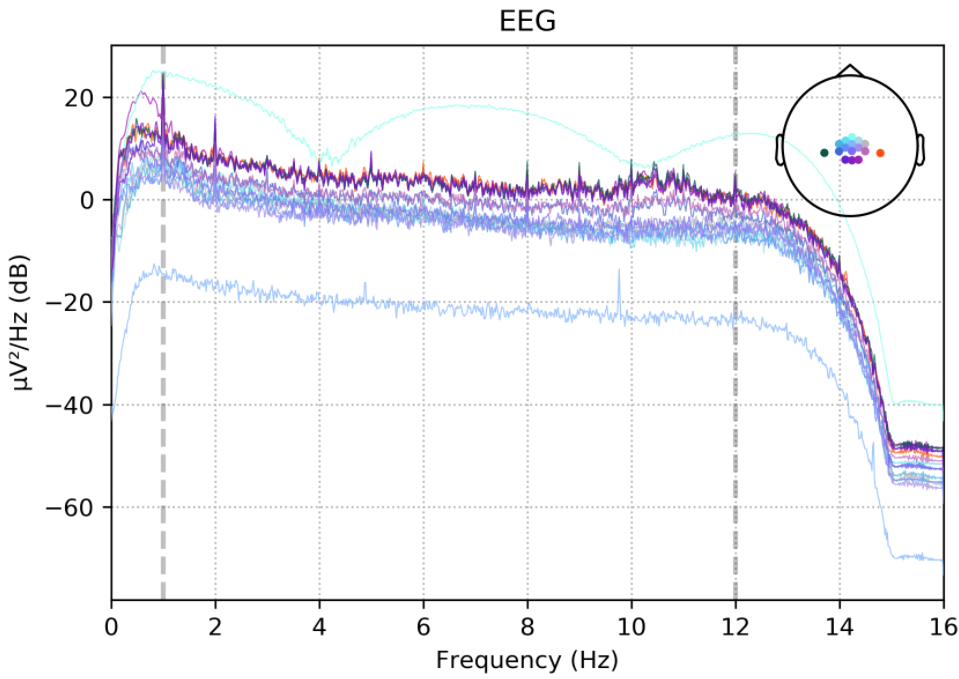
配置二功率谱密度图

配置三

  • 21导联 [P7,P5,P3,P1,PZ,P2,P4,P6,P8,PO7,PO5,PO3,POZ,PO4,PO6,PO8,CB1,O1,OZ,O2,CB2]
  • 降采样至200HZ，1-20Hz滤波
tot_channel=['FP1', 'FPZ', 'FP2', 'AF3', 'AF4', 'F7', 'F5', 'F3', 'F1', 'FZ', 'F2', 'F4', 'F6', 'F8', 'FT7', 'FC5', 'FC3', 'FC1', 'FCZ', 'FC2', 'FC4', 'FC6', 'FT8', 'T7', 'C5', 'C3', 'C1', 'CZ', 'C2', 'C4', 'C6', 'T8', 'M1', 'TP7', 'CP5', 'CP3', 'CP1', 'CPZ', 'CP2', 'CP4', 'CP6', 'TP8', 'M2', 'P7', 'P5', 'P3', 'P1', 'PZ', 'P2', 'P4', 'P6', 'P8', 'PO7', 'PO5', 'PO3', 'POZ', 'PO4', 'PO6', 'PO8', 'CB1', 'O1', 'OZ', 'O2', 'CB2', 'HEO', 'VEO', 'EKG', 'EMG']
need_channel=['P7','P5','P3','P1','PZ','P2','P4','P6','P8','PO7','PO5','PO3','POZ','PO4','PO6','PO8','CB1','O1','OZ','O2','CB2']
drop_channels=[ item for item in tot_channel  if item not in need_channel]
sig_rate=200
data,times=load_data(filename,sig_rate,drop_channels,1,20)

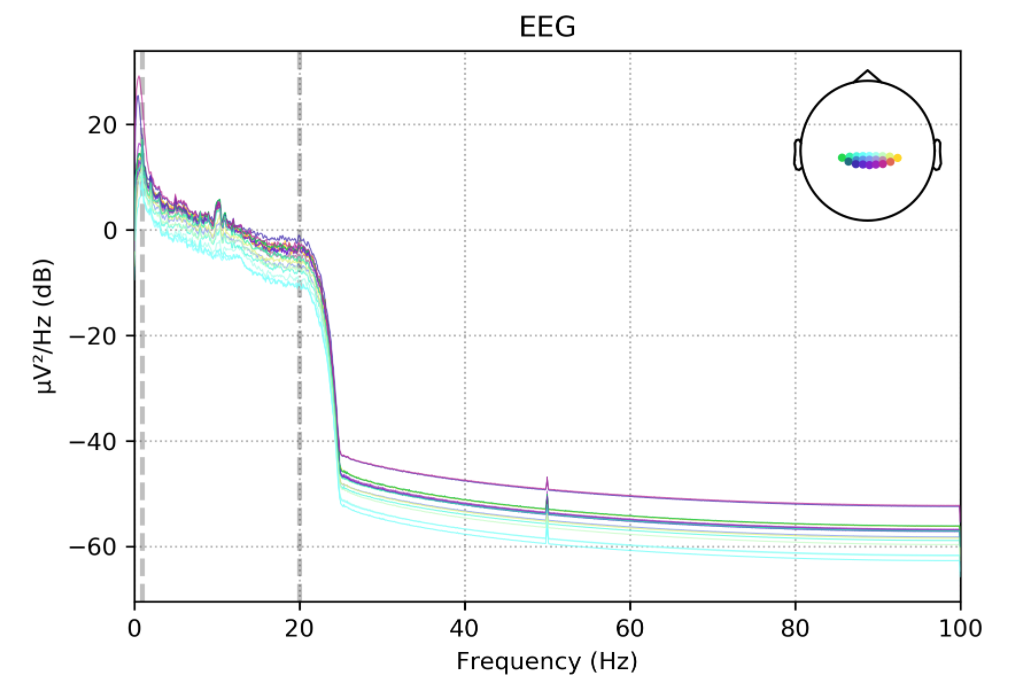
配置三功率谱密度图

数据预处理

把时间序列数据从里面一块块摘出来，并且打上标签。

labels_train=[]
signals_train=[]
sa1=[]
sa2=[]
eeg=data
mv=int(-0.175*sig_rate) #偏移
k_fos = 0
for i in range(11):
    dp_start = mv+i * 180 * sig_rate
    s2 = 0
    for j in range(160):
        if i==0 and j==0:
            continue
        btime=int( dp_start+j*sig_rate)
        etime=int(dp_start+(j+1)*sig_rate)
        dataTrain = eeg[:,btime:etime]
        signals_train.append(dataTrain)
        if clicktime[k_fos]<etime*1000/sig_rate and clicktime[k_fos]>=btime*1000/sig_rate:
            labels_train.append(1)
            sa1.append(dataTrain)
            k_fos += 1
        else:
            labels_train.append(0)
            sa2.append(dataTrain)
test_x=[]
test_y=[]
for i in range(11,12):
    dp_start = mv+i * 180 * sig_rate
    for j in range(160):
        btime=int( dp_start+j*sig_rate)
        etime=int(dp_start+(j+1)*sig_rate)
        dataTrain = eeg[:,btime:etime]
        test_x.append(dataTrain)
        if j in target_list[i]:
            test_y.append(1)
        else:
            test_y.append(0)
print(len(signals_train))
print(len(test_x))

上面运行后就可以根据输出结果reshape,当然也可以直接变量传递，我比较喜欢看一下进行后面的。

signals_train=np.array(signals_train).reshape((1759,-1))
test_x=np.array(test_x).reshape((160,-1))
print(signals_train.shape)

数据的归一化训练集测试集的划分

from sklearn import svm
import sklearn
from sklearn.preprocessing import StandardScaler
Stan_scaler = StandardScaler()
signals_train= Stan_scaler.fit_transform(signals_train)
train_data,test_data,train_label,test_label =sklearn.model_selection.train_test_split(signals_train,labels_train, random_state=2, train_size=0.9,test_size=0.1)

调用SVM进行分类器的训练

classifier=svm.SVC(C=0.9,kernel='rbf',decision_function_shape='ovr',class_weight='balanced',probability=True) # ovr:一对多策略
classifier.fit(train_data,train_label)

输出结果如下

SVC(C=0.9, cache_size=200, class_weight=’balanced’, coef0=0.0,
decision_function_shape=’ovr’, degree=3, gamma=’auto’, kernel=’rbf’,
max_iter=-1, probability=True, random_state=None, shrinking=True,
tol=0.001, verbose=False)

拿测试集进行预测并检验结果

from sklearn.metrics import accuracy_score
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score

tra_label=classifier.predict(train_data) #训练集的预测标签
tes_label=classifier.predict(test_data) #测试集的预测标签
print("训练集：", accuracy_score(train_label,tra_label) )
print("测试集：", accuracy_score(test_label,tes_label) )
print("测试集精确率（预测为正的样本中有多少是真正的正样本。）：",precision_score(test_label,tes_label))
print("测试集召回率（样本中的正例有多少被预测正确了。）：",recall_score(test_label,tes_label))
tes_label

输出结果如下

  • 训练集： 0.9993682880606444
  • 测试集： 0.9886363636363636
  • 测试集精确率（预测为正的样本中有多少是真正的正样本。）： 1.0
  • 测试集召回率（样本中的正例有多少被预测正确了。）： 0.6666666666666666

这里是对于有人工参与点击鼠标进行的标签用于测试模型。也就是说这个标签的实质是人脑是否有波动，而非该时间段是否有目标出现。
因为人脑检测到的目标不一定是正确的目标，但是训练的时候需要以人脑是否有波动为准。
可以看到在精确率表现不错（样本其实还是比较少，不然没那么高）。

最后看看实际操作

tes_label=classifier.predict(Stan_scaler.transform(test_x))
print("测试集精确率（预测为正的样本中有多少是真正的正样本。）：",precision_score(test_y,tes_label))
print("测试集召回率（样本中的正例有多少被预测正确了。）：",recall_score(test_y,tes_label))
  • 测试集精确率（预测为正的样本中有多少是真正的正样本。）： 1.0
  • 测试集召回率（样本中的正例有多少被预测正确了。）： 0.06666666666666667

这里的标签就是该时间段是否有目标呈现，也就是真正应用场景中的精确率。
可以看到精确率还是挺高的，但是也存在问题，那就是召回率太低了，它只找到了很小一部分目标，很可能是瞎猫碰到死老鼠，具体问题出现在哪里还是要看后续研究了。

文章作者: 青椒
文章链接: https://zhkgo.github.io/2020/09/10/rsvp20200910/
版权声明: 本笔记所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 青椒 !
脑电信号 RSVP 事件相关电位
 上一篇
EEGNET网络结构解析与复现 EEGNET网络结构解析与复现
脑机接口(BCI)使用神经活动作为控制信号，实现与计算机的直接通信。这种神经信号通常是从各种研究透彻的脑电图(EEG)信号中挑选出来的。卷积神经网络(CNN)主要用来自动特征提取和分类，其在计算机视觉和语音识别领域中的使用已经很广泛。CN
2020-11-19 青椒
脑电信号 深度学习 paddlepaddle
下一篇 
基于Pierre Dellacherie算法玩俄罗斯方块 基于Pierre Dellacherie算法玩俄罗斯方块
这个算法更加注重俄罗斯方块的不死性，如果用遗传算法或者模拟退火算法训练好权重后能够达到很好的效果。主要参考https://blog.csdn.net/qq_41882147/article/details/80005763进行设计。 评
2020-09-03 青椒
俄罗斯方块
  目录